WTF - 3. Maybe or Not
What is the Functional?
Maybe
바로 앞에서 언급했듯이 최근에 생겼거나 메이저 업데이트를 한 언어들이라면 대부분 지원하는 Maybe(Optional, Option)라는 타입이 있다. 값을 가지고 있는 Just라는 타입과 값이 없는 Nothing이라는 타입 중 하나가 되는 섬 타입이다. 일단 함수형이니 하는 이야기는 잠시 미뤄두고 간단하게 Maybe를 만들어보자. Maybe의 정의를 간단하게 표현해보자면 다음과 같다.
1 | data Maybe a = Just a | Nothing |
1 | class Maybe { |
정의는 단순하지만 같은 내용을 JavaScript로 구현하면 다소 길어진다. 소스를 보면 알겠지만, Just는 생성될 때만 값을 받을 수 있고 생성된 후에는 값을 변경할 수 없다. 이제 이 Maybe를 어떻게 다룰지에 대해서 생각을 해보자. Maybe 타입을 통해 어떤 연산을 하고 싶을 때 메소드를 추가해서 Maybe를 계속 생산하도록 만들면 편하겠지만, 값이 있다 없다의 속성을 가질 수 있다면 Maybe의 연산 결과를 Maybe라고 유지하고, 값이 없을 때는 계속 값이 없도록 유지하려면 그 결괏값을 보장해줘야한다. 이걸 만족하는 연산들을 생각해보자.
- 값을 Maybe로 감싸서 새로운 Maybe를 만들어준다.
- Maybe의 값에 그 값을 처리하는 함수를 적용하고 싶다.
- 그런데 그 함수가 Maybe의 값일 수도 있다.
- 함수의 결괏값 자체가 Maybe라면 어떨까?
1번의 구현은 간단하다.
1 | ///// unit : a -> Maybe a |
값만 존재할 때는 두 배로 만들려면 단순히 x * 2를 하면 되지만, Maybe로 감싸져
있으니 바로 적용하기 어렵다. 그러니 2번처럼 값을 처리하는 함수를 적용할 수 있는
기능을 구현해보자.
1 | const isNothing = (m) => |
Maybe의 값이 함수일 경우에 그 함수를 다른 Maybe의 값에 적용해보자.
1 | ///// appl : Maybe (a -> b), Maybe a -> Maybe b |
그런데 모양을 보면 fmap과 비슷해서 fmap을 재사용해서 구현할 수도 있다.
1 | const appl2 = (mfn, ma) => |
이제 마지막으로 함수의 결과 자체가 Maybe일 경우를 생각해보자.
1 | ///// bind : Maybe a, (a -> Maybe b) -> Maybe b |
지금까지의 구현에서 JavaScript 자체의 복잡한 기능을 사용한 곳은 없다. 구현
자체가 어렵지도 않고 짧아서 여기까지는 다들 이해할 수 있을 것으로 생각한다.
그런데 안에 값을 넣을 수 있는 타입 중에서 개발자들이 항상 사용하고 있으며,
다들 사용법에 대해 아주 잘 알고 있는 타입이 하나 있다. 이제 Maybe를 Array와
비교해보자.
F, A, M with Array
1. Functor
앞에서 구현했던 fmap에서 설명을 돕기 위해 구현 위에 주석으로 타입을 적어놓은
것이 있다. 처음에는 Haskell 식으로 타입을 적었다가 이해하기 편하도록 수정했더니
무슨 언어인지 모를 내용이 되긴 했지만.
1 | ///// fmap : Maybe a, (a -> b) -> Maybe b |
값을 가지고 있는 타입과 값을 변환하는 함수를 받아서 다른 값을 가지고 있는 타입으로 변환해준다. 이걸 이해하기 좋게 조금 수정해보자면,
1 | ///// amap : Array a, (a -> b) -> Array b |
a라는 타입의 값을 가지고 있는 어떤 타입을 ⓐ라고 하고, b의 경우를 ⓑ라고 하면,
(a -> b) 함수를 통해 결과적으로 (ⓐ -> ⓑ)를 만족하도록 연산할 수 있는 타입을
Functor라고 부른다. Array에서는 그런 연산을 해주는 map 메소드를 가지고 있다.
2. Applicative Functor
순서대로 fmap 다음에 구현했던 appl을 이야기할 차례다.
1 | ///// appl : Maybe (a -> b), Maybe a -> Maybe b |
applicative라는 표현 그대로 어딘가에 적용할 수 있는 Functor이다. 즉, 함수를 가지고 있는 Functor.
1 | const doub = d => d * 2; |
이렇게 (a -> b)를 가지고 있는 Array와 Array a를 통해 Array b를 만들었다. 위에서
말했듯 함수를 가지고 있는 Functor(Array (a -> b))와 다른 Functor(Array a)를 통해
다른 Functor(Array b)를 만들어내는 Applicative Functor를 map을 사용해서 간단히
구현해보았다. 하지만 Applicative Functor 자체를 본 적이 별로 없어서 내가 맞게
이해하고 있는 것인지 잘 모르겠다.
3. Monad
1 | ///// bind : Maybe a, (a -> Maybe b) -> Maybe b |
JavaScript에서는 lodash같은 라이브러리를 사용하지 않은 사람에게 익숙하지 않은 개념일 수 있지만, 다른 함수형 언어들을 써본 사람이라면 Sequence 종류에서 기본적으로 지원해주는 익숙한 개념이 있다.
1 | const flatMap = function(fn) { |
바로 flatMap(간혹 concatMap)이라는 개념인데, (a -> ⓑ) 함수를 통해
(ⓐ -> ⓑ)를 만족하는 함수를 말한다. [1, [2], [[3]]]처럼 깊이가 다른 배열을
1차원으로 합치는 함수를 flatten이라고 표현하는데, flatten + map이 아닐까 싶다.
Haskell에서는 Monad라면 Applicative Functor를 만족하고, Applicative Functor라면
Functor를 만족한다. 즉 Monad > Applicative > Functor로 상속하는 구조다. 잠깐
접해본 짧은 생각으로는 독립적인 개념으로 봐도 될 것 같은데(굳이 따지자면
Functor와 Applicative 정도는 has-a로 봐도 될 것 같지만), 내가 놓치고 있는 뭔가가
있는 것 같다.
이렇게 대수형 타입끼리 어떻게 연산하는지의 패턴들에 대해 알아봤는데, 왜 이렇게 복잡한 설명과 패턴을 통해 타입을 유지해야 하는가 싶은 생각이 들 수 있다. 가장 기본이 되는 개념은 간단한 개념이니 이것만 알면 된다! 라는 식의 글을 참 많이 봤는데, 내가 원점에 있을 때 (10, 0)쯤에 있던 글보다 쉽다는 글은 (0, 10)쯤에 있었고 그보다 쉽다고 주장하는 글은 (-10, 0)쯤에 있었다. 방향만 달라질 뿐, 거리는 좁혀지지 않는 느낌이었다. 그래도 그나마 알아들을만 했던 예제는 Railway oriented Programming이었다.
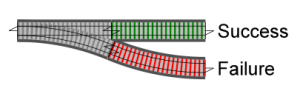
Just에 어떤 연산bind을 할 때 결과는 다시 Maybe가 되어야 하니 Just(그림에서의
Success) 혹은 Nothing(그림에서의 Failure) 둘 중 하나가 된다.
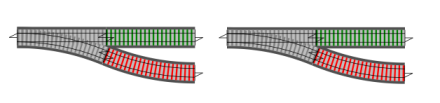
그런 연산이 여러 개 존재할 수 있다.
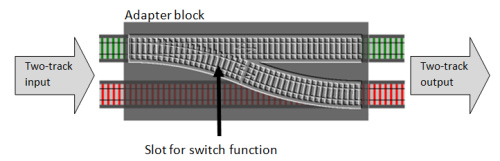
그때, 앞에서 어떤 처리들이 있었고 어디에서 Nothing으로 갔는지 관계없이 현재 들어온 값을 보고 Just인지 Nothing인지 구분(switch)해주는 하나의 블럭을 만들기만 하면 된다.

한번 Nothing이 되면 그 뒤에 어떤 연산이 오든 관계없이 Nothing으로 계속
유지된다. 앞의 어디에서 Nothing이 되었다는 것에 신경 쓰지 않고 현재의 값만 보고
Just인지 Nothing인지 연결하면 된다. 즉, bind(혹은 flatMap)에서는 현재 값과
앞뒤 타입만 맞추면 입력에서 출력까지 연산이 안전하다고 보장된다.
패턴이라는 것은 약속이고, 약속이라는 것은 그것이 보장된다는 말이다. 즉 일종의 추상화로 블랙박스 모델처럼 그림에서의 스위치만 구현해서 레일을 연결하면 안전하게 연산이 잘 흘러간다. OOP처럼 객체 단위의 추상화가 없으니 타입클래스에서 이런 패턴들이 그 역할을 대신하고, 덕분에 재사용하기 좋고 확장 가능해진다. 그런 것들의 기초가 되기 때문에 사람들이 중요하다고 많이 이야기하는 것이라고 생각한다.
여전히 이게 뭐다라고 정의내려서 설명하기는 어렵지만 이제 A가 B다라는 말에서 그게 맞거나 틀리다는걸 구분할 수는 있는 것 같다. 사실 이 글을 쓰게 된 목적 중 하나는 이거다. 그동안 함수형 언어를 기껏해야 퀴즈 몇개 풀어보는 정도 이외에는 제대로 써본 적이 없다보니 알듯말듯 한 상태가 몇년째 계속되고 있는데, 최근에 Haskell 책 한권을 읽으면서 그 감이 약간 더 구체화된 김에 정리를 해서 더 잡기 위해서다. 물론 조금 어긋난 내용이 있을 수도 있고 아예 잘못된 내용이 있을 수 있어서 언젠가 이 글을 읽고 이불킥할지도 모르겠지만, 이번 기회에 정리하지 않으면 몇년 더 이해할 기회가 오지 않을 것같다는 느낌이 들었다. 그러니 틀린게 있으면 틀린거고, 아니면 좋고. 이제 Monad라는게 뭔지 대충 정리를 해밨으니 이걸로 뭘 할 수 있는지 한번 써먹어보자.
ps, 타입을 유지하기 위한 연산의 패턴들에 대해서 알아봤는데 이런 것들이 타입론 (Type Theory)이나 범주론(Category Theory)에 속한 것이라면, "정수의 덧셈은 정수에 '닫혀있다'"라고 말하는 것처럼 연산 자체의 성질에 대해서 논하는 군론(Group Theory)라는 것이 있고 그 중 모노이드(Monoid)라는 개념을 모나드와 함께 사용하면 더 편하게 사용할 수 있는데 그 부분에 대해서는 지금보다 아는 것이 좀 더 생기면 다뤄보고 싶다.
ps2, 다시 말하지만 ps도 맞는지 확신이 없다.
Reference
-
Hackage: Official Haskell Package archive
-
Codewars Kata
- Monads: The Maybe Monad : Maybe = Just | Nothing
-
All Image Credit under CC BY 3.0 by ScottWlaschin